「33」Float IEEE标准

发表于 本文字数： 1.4k 阅读时长 ≈ 1 分钟

前序

前几天踩坑Float类型的计算问题,今天来系统的总结下float相关的知识点.

掌握关键点:

  • float的标准是什么?
  • float的位计算规则
  • float场景
  • float计算改进

Float的标准?

国际组织定义

wiki–>float定义

表示方法

  • value: 实际值
  • sign bit: 符号位
  • exponent bit: 指数便宜位
  • fraction: 分数值

具体表示:

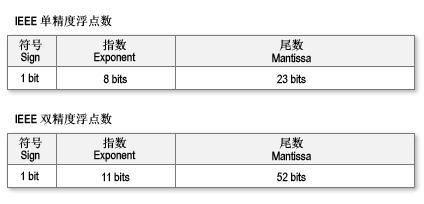
单精度和双精度

特殊值:

  • 无穷: Inf
  • 非数值: NaN

Float位计算规则

原码

  • 高位表示符号位,其余为值; ⚠️:不能直接参与计算

反码

  • 正数反码为本身
  • 负数保留符号位,其它位按位取反.
1
2
3
例如 :
[+7]原 = 00000111 [+7]反 = 00000111 
[-7]原 = 10000111 [-7]反 = 11111000

补码

  • 正数的补码==原码==补码
  • 负数补码=反码+1

计算形式:

说明:
  • 表示符号位
  • M表示有效数字
  • 表示指数位
1
2
3
4
5
eg:
-0.5 => -0.1[二进制]
=> -1.0 * 2^-1
=> (-1)^1 * 1.0 * 2^-1
=> s=1，M=1.0，E=-1

float类型的加法:

  • 对阶
  • 尾数
  • 规格化
  • 舍入处理
  • 溢出判断

1
2
3
a=(0.3)10=(0011 1110 1001 1001 1001 1001 1001 1010)2    Sa=0    Ea=011 1110 1    Ma=1.001 1001 1001 1001 1001 1010

b=(1.6)10=(0011 1111 1100 1100 1100 1100 1100 1101)2      Sb=0    Eb=011 1111 1     Mb=1.100 1100 1100 1100 1100 1101
对阶

简单的说就是需要阶码对齐,使其尾数可以进行加减运算,即:

$ ⊿E = E_b -E_a $

1
2
3
4
5
Ea<Eb   Eb-Ea=2

Ma要调整为 0.0 1001 1001 1001 1001 1001 10       10

E=011 1111 1
尾数
1
2
3
4
  0.01001100110011001100110
+ 1.10011001100110011001101
----------------------------
  1.11100110011001100110011
规格化

尾数的格式 $ 1.M $,尾数可能是非规格化的,所以需要左规和右规操作:

  • 左规操作: 尾数左移,阶码减值
  • 右规操作: 尾数右移,阶码+值

$ 目的: 1 \leq M < 2 $

舍入处理

四种舍入方式:

  • 就近舍入: 四舍五入
  • 朝+∞舍入
  • 朝-∞舍入
  • 朝0舍入
1
2
3
在对阶时，Ma有右移，且第一次最高为1，第二次为0，
所以按"0舍1入"， ==> 精度丢失的关键, 
尾数运算结果调整为 1.11100110011001100110100
溢出判断

判断结果标准: 运算结果的阶码

1
2
3
4
5
6
a+b=(0  01111111  11100110011001100110100)2
=(0011 1111 1111 0011 0011 0011 0011 0100)2=(3FF33334)16

转为10进制

a+b=1.90000010

float计算改进

尽量避免使用高精度且重要的数据计算: 如: ¥

统一取舍位数

  • 统一保留
  • 统一取舍算法

建议用int/string类型

  • 缺点:
    • 牺牲性能
    • 转换复杂
  • 优点:
    • 提高准确度
    • 处理可多元化